L'impedenza elettrica è una misura della resistenza e della reattanza combinata di un circuito elettrico. È una grandezza che descrive l'opposizione offerta da un circuito elettrico al passaggio della corrente alternata.
Questo articolo fornisce una spiegazione approfondita sull'argomento e come viene utilizzata nell'elettronica.

Sia la corrente continua che la corrente alternata percorrendo un induttore il cui avvolgimento è costituito da numerose spire di filo di piccola sezione, quindi con una resistenza molto alta, incontrano un ostacolo dovuto da tale resistenza.
La corrente alternata, oltre a questa resistenza, incontra anche l'ostacolo dovuto alla reattanza induttiva che si comporta sia come un induttore che come un resistore.
Nella Fig. 1 è rappresentato un induttore senza resistenza (con resistenza trascurabile) e nella Fig. 2 un induttore con resistenza collegato in serie alla parte induttiva.
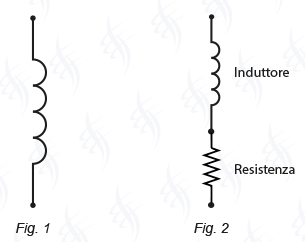
Nella Fig. 2, ai due estremi, è presente la stessa induttanza e la stessa resistenza presentata dall'induttore quindi tali punti si devono considerare come estremi dell'induttore con resistenza.
Osserviamo ora la Fig. 3
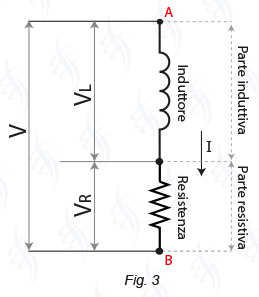
Se non fosse presente la parte resistiva l'avvolgimento non presenterebbe resistenza quindi per far circolare una corrente alternata di un determinato valore efficace basterebbe applicare alla parte induttiva la tensione indicata con VL
Visto che l'avvolgimento presenta anche una resistenza, per far circolare una corrente occorre applicare alla parte induttiva dell'induttore anche la tensione indicata con VR
Questo farebbe pensare che tra gli estremi A e B occorre applicare una tensione V con valore efficace dato dalla somma delle due tensioni, VL + VR
Ciò invece non avviene perchè le tensioni VL e VR non hanno la stessa fase rispetto alla corrente. Mentre la tensione VR è in fase con la corrente, la tensione VL è sfasata in anticipo di un quarto di periodo rispetto alla corrente.

Nei tre grafici sono mostrati due cicli della corrente I, della tensione VR e della tensione VL mediante due sinusoidi (la seconda è di colore verde).
Come si può notare la tensione VR è in fase con la corrente perchè entrambe le sinusoidi iniziano e terminano nello stesso periodo. Confrontando invece la sinusoide della corrente I con la sinusoide della tensione VL si nota che quest'ultima è sfasata in anticipo di un quarto di periodo rispetto alla corrente infatti la seconda sinusoide (colore verde) inizia e termina un quarto di periodo prima della seconda sinusoide (colore verde) della corrente I
Da ciò, la tensione VL che occorre per la parte induttiva dell'induttore è sfasata in anticipo di un quarto di periodo rispetto alla tensione VR che occorre per la parte resistiva dello stesso induttore.
Per questo sfasamento, nell'istante in cui una delle due tensioni assume il valore massimo, l'altra assume il valore nullo e viceversa quando una delle due assume il valore nullo l'altra assume il valore massimo. Ciò si può constatare nella Fig. 4 infatti mentre a 0s la tensione VR è nulla la tensione VL ha il valore massimo invece a 0,05s mentre la tensione VL è nulla la tensione VR assume il valore massimo.
Questo comporta che il valore massimo della tensione V della Fig. 3 non è dato dalla somma dei due valori massimi raggiunti dalle tensioni VR e VL perchè, come abbiamo visto precedentemente, le due tensioni, VR e VL, raggiungono i valori massimi in momenti diversi.
Passiamo a rappresentare vettorialmente la corrente e le tensioni relative ad un induttore con resistenza:
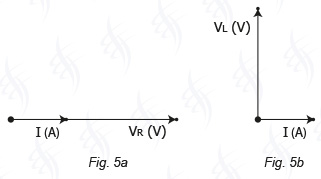
Per riunire in un'unica rappresentazione tutte le grandezze relative all'induttore con resistenza basta sovrapporre le due rappresentazioni vettoriali, Fig 5 a e Fig 5 b, in modo che i vettori che rappresentano la medesima corrente risultino coincidenti (Fig. 6).
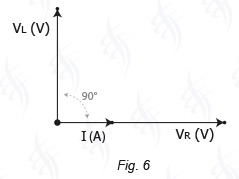
Come già spiegato, per trovare il valore massimo della tensione V della Fig. 3 non è possibile sommare i valori massimi delle tensioni VR e VL questo perchè si deve tenere conto dello sfasamento di cui abbiamo parlato prima.
Il vettore che rappresenta la tensione V da applicare agli estremi A e B della Fig. 3 si può invece ottenere sommando i vettori che rappresentano le tensioni VR e VL questo perchè i vettori, oltre a rappresentare con la loro lunghezza il valore massimo delle due tensioni, con il senso in cui sono diretti indicano anche lo sfasamento che esiste tra le due tensioni.
Disegnando graficamente i due vettori VR e VL mantenendo il verso in cui sono diretti, orizzontale per il vettore VR e verticale per il vettore VL, e unendo i punti dei due vettori si ottiene il vettore che rappresenta la loro somma (Fig. 7) che rappresenta la tensione V da applicare all'induttore con resistenza.

Osservando la Fig. 5b e la Fig. 7 si può notare che non è stato alterato l'angolo di sfasamento di 90° compreso tra i due vettori.
Visto che i tre vettori formano un triangolo rettangolo il valore massimo della tensione V si può trovare applicando il teorema di Pitagora.
Il teorema di Pitagora stabilisce che in un triangolo rettangolo il quadrato della misura dell'ipotenusa è uguale alla somma dei quadrati delle misure dei cateti:
i² = C1² + C2²
Quindi la somma dei quadrati delle tensioni VR e VL è uguale al quadrato della tensione V
V² = VR² + VL²
Per ottenere il valore della tensione V si deve estrarre la radice quadrata di V²:
V = √V²
Il valore massimo di una corrente alternata è uguale a 1,41 volte il valore efficace quindi: il valore efficace della tensione da applicare agli estremi di un induttore con resistenza è uguale alla radice quadrata del numero ottenuto sommando i quadrati dei valori efficaci delle tensioni occorrenti per la parte induttiva e per la parte resistiva dell'induttore
V = √VR² + VL²
La parte resistiva e quella induttiva dell'induttore presentano un ostacolo alla corrente che le attraversa, impedenza elettrica (Z) che, come la resistenza e la reattanza, si misura in Ohm (Ω)
L'impedenza elettrica Z si ottiene estraendo la radice quadrata della somma dei quadrati della resistenza e della reattanza
Z = √R² + XL²
L'impedenza si può quindi utilizzare nell'impiego della legge di Ohm: da ciò per ottenere la tensione necessaria per far attraversare un induttore con resistenza da una determinata corrente alternata si moltiplica l'impedenza presentata dell'induttore per la corrente
V = Z x I






